A modern laptop can run ~3.8 billion cycles per second. The cycle is determined by oscillation frequency of the electrical signal that hits the CPU. Contemporary CPUs manage synchronisation using all sorts of error correction tricks.

In mechanical systems, such as those used in medical equipment and robotics, the binary numbers that we are most familiar with can cause errors if they're read during state transition.

Decimal and Binary

We are most familiar with decimals, this is a base 10 counting notation where each position in the number represents a different power of ten. E.g. 10, 100, 1000.

The computer relies on binary as this takes advantage of the fundamental on/off state within an electronic circuit. Binary is base 2, so each position represents a power of 2. E.g. 2, 4, 8, 16.

Reading States

Binary numbers can cause errors if they're read during transitions. The more positions that require toggling, while switching between numbers, the higher the chance we introduce errors into the system. This is shown clearly as we transition between the numbers 3 and 4. Which requires changing three bit positions. 011 -> 100.

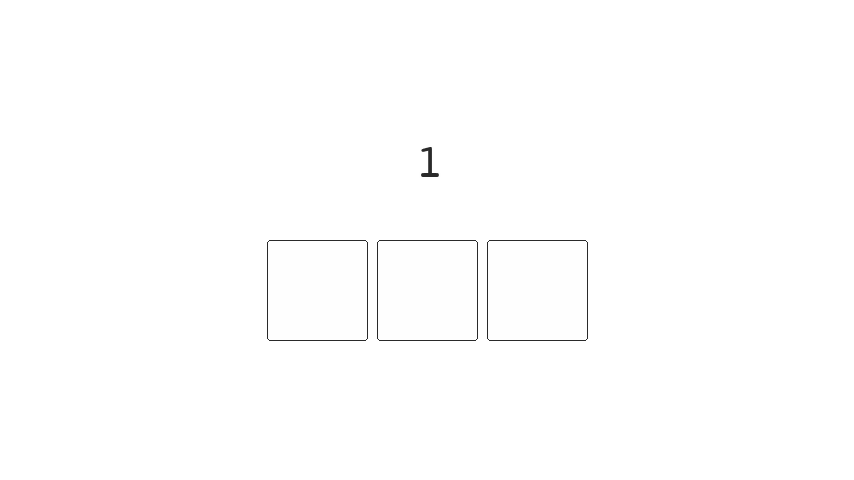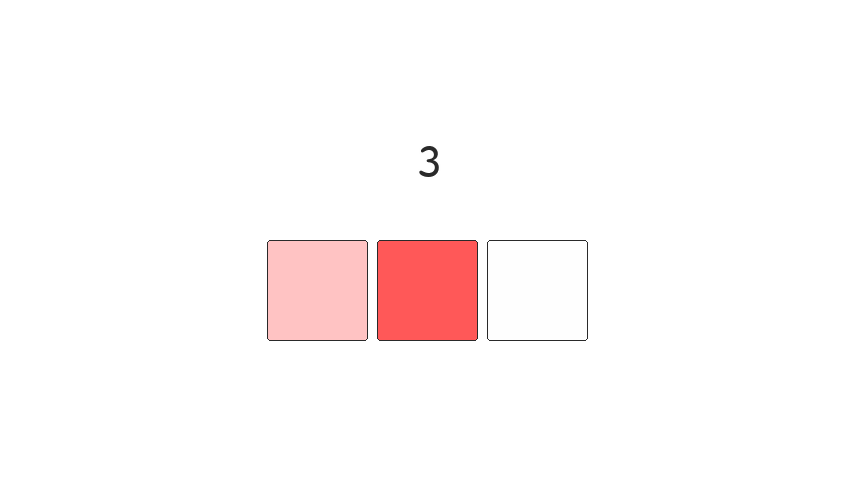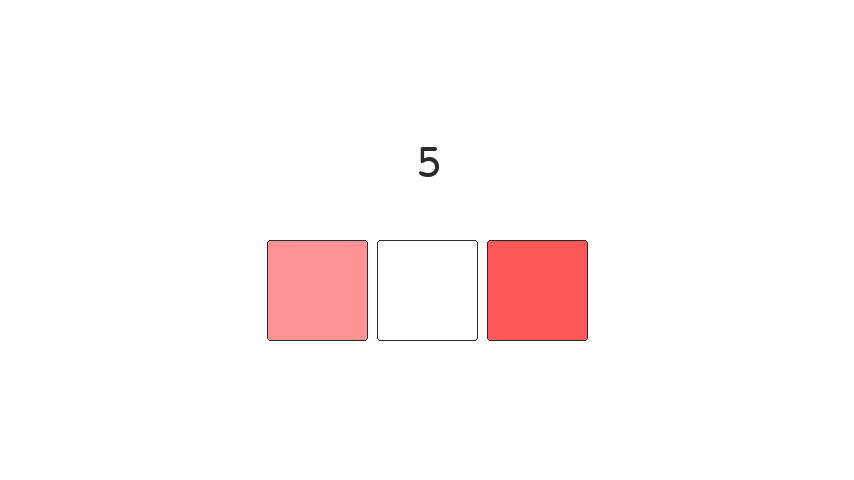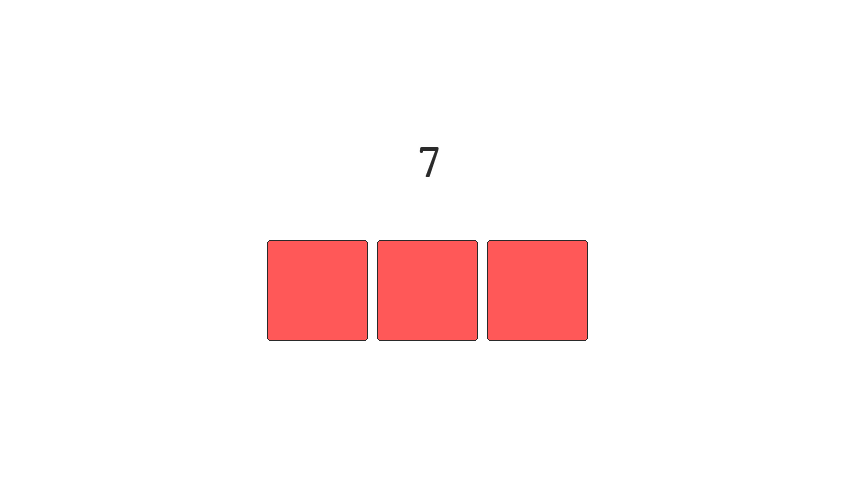
If these bits aren't switched instantly we can read any of the following numbers 1, 2, 5, 6 or 7 instead of 3 or 4. Not great if you're working with a critical system and need precision.

Grey Code

To get around this we use an alternative ordering of the binary system in which successive numbers are separated by a single bit. Incrementing a number only relies on switching one position and removes the chance of reading the wrong number during state transitions.

This ordering is called Gray code, and an animation of the bit positions, for an incrementing number, is shown below:

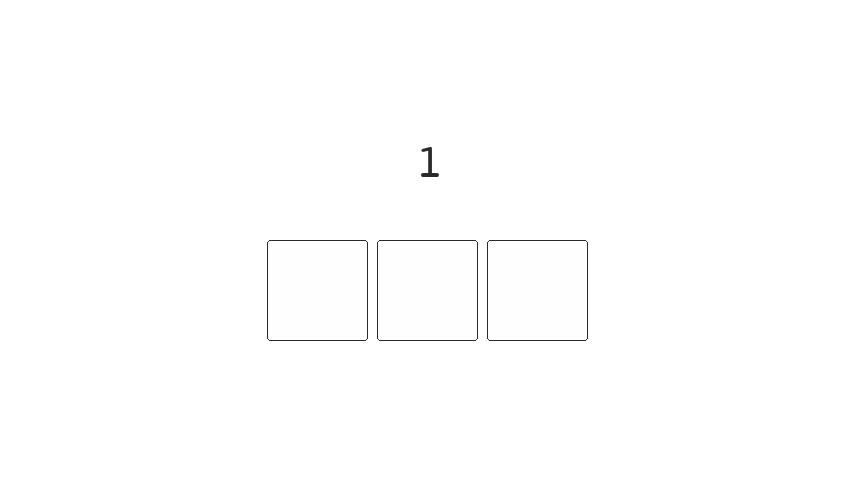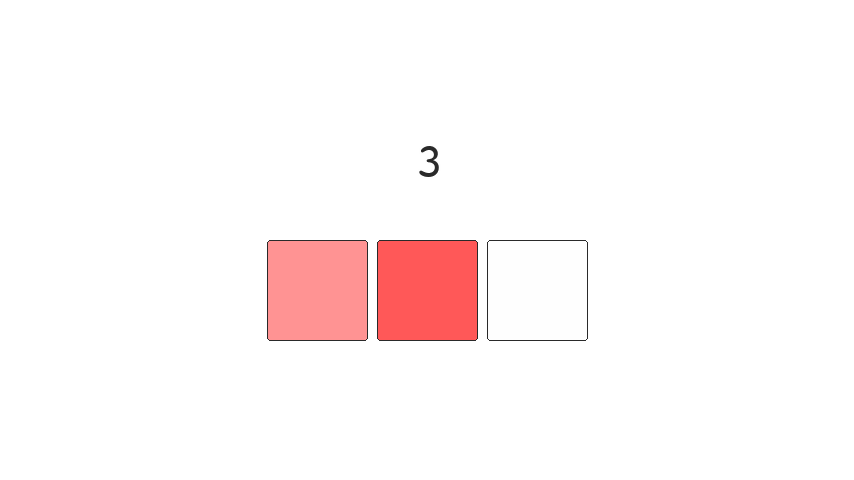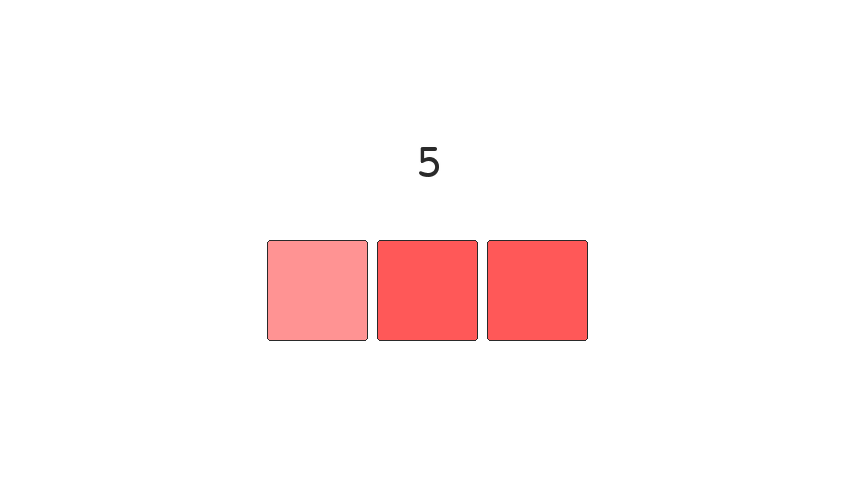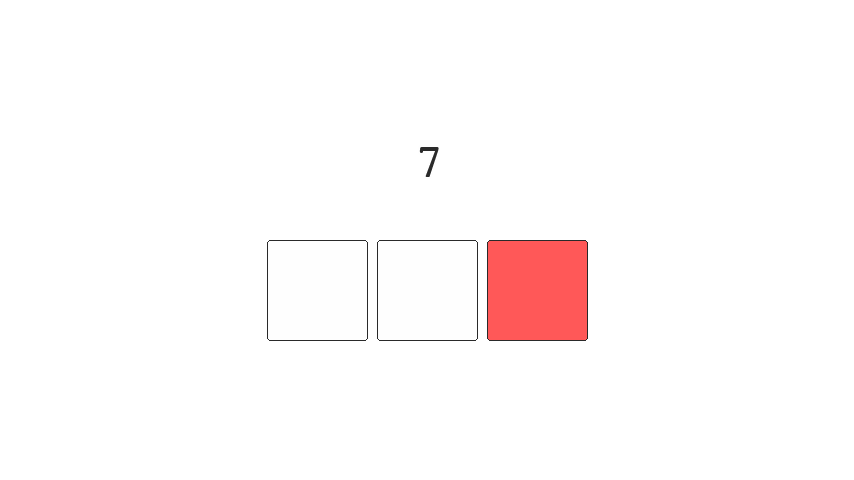
Decimal	Binary	Gray
0	0000	0000
1	0001	0001
2	0010	0011
3	0011	0010
4	0100	0110

The Application

In addition to reducing read errors, relying on only a single toggle to move up the number scale consumes less energy than traditional binary due the fewer toggled bits.

Some systems require testing every position of multiple switches or toggles. Gray code can improve the efficiency of these tests. If we had to iterate through all 16 combinations of 4 switches. Using ordinary binary would need to flip 1, 2, 1, and then 3 toggles as we move from numbers 1 to 4, while gray code allows us to only ever need to flip a single toggle to eventually test all switch combinations.

One of the most common uses of gray code is in rotary encoders, also known as knobs. These convert angular position to an analog or digital signal. If we had to rely on a normal binary scale, when rotating the knob, it could end up sending the intermediary numbers between each angle, which would make it pretty useless.