On May 24th 2000 the Clay Math Institute announced a $1,000,000 prize for solving one of 7 maths problems. Since then only 1 has been solved. The mathematician that solved the problem rejected the money.¹

One of those problems is the P vs NP question which relates to how we estimate time and space complexity for algorithms in computer science and software engineering.

Complexity

Complexity is an estimate of the growth in either time or space given an increase in the size of the input. Some algorithms have a linear relationship between time and input, we signify this complexity as O(n).

Constant complexity is signified as O(1) this means that as we increase n (the size of the input) the time and space is consistent, the algorithm doesn't take any longer and doesn't require more RAM.

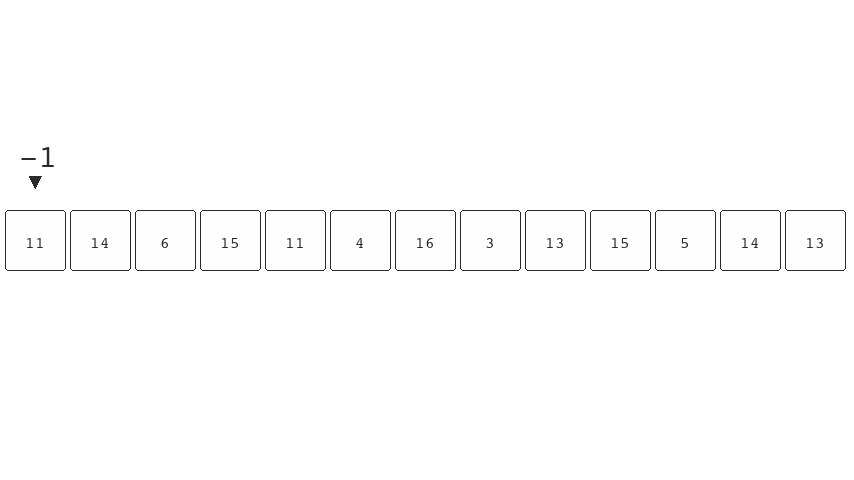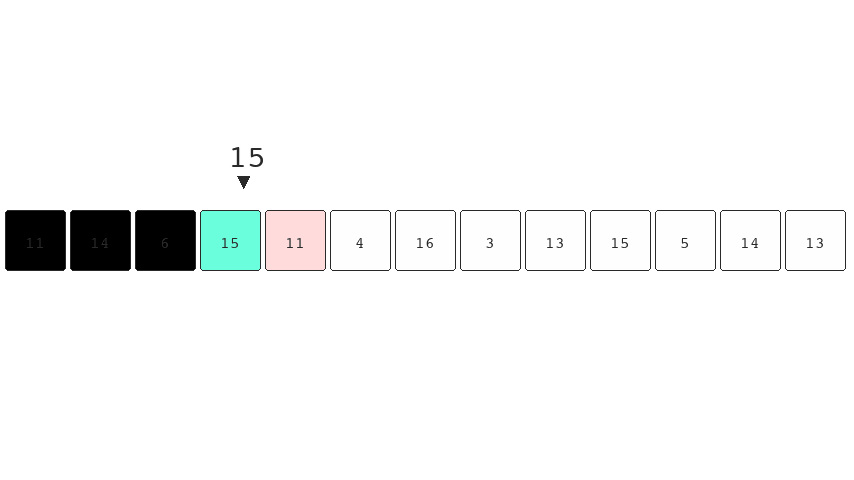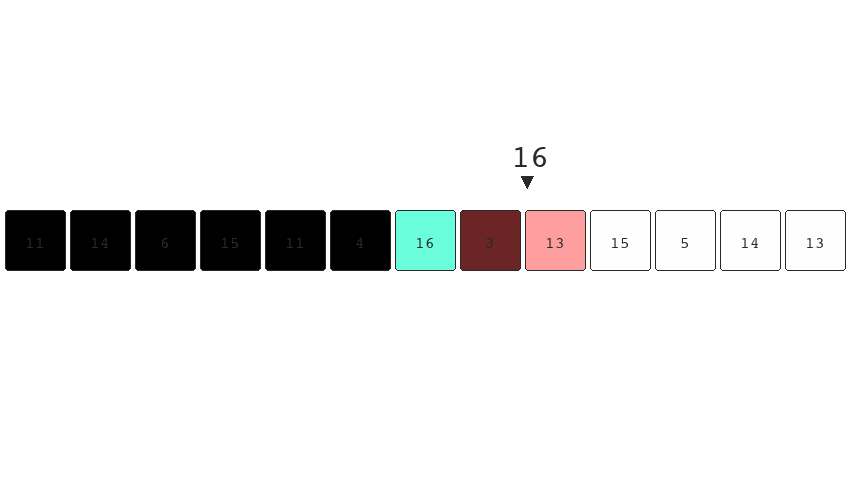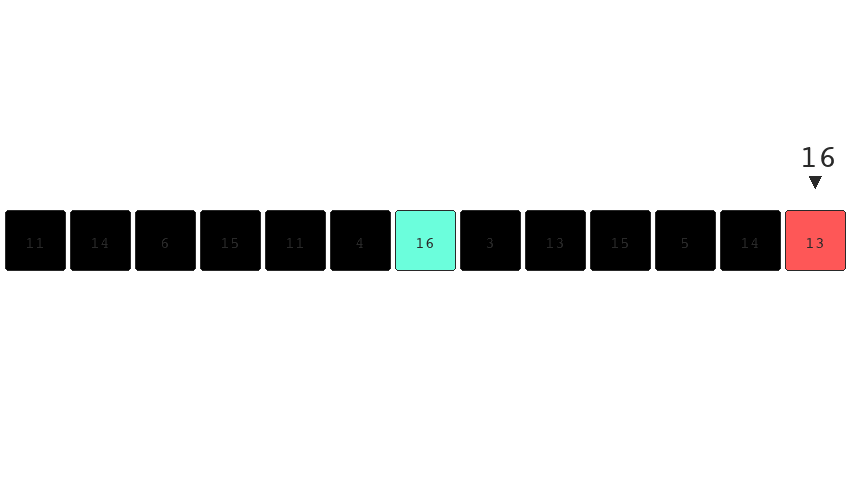
An example of an algorithm that take constant O(1) space is finding the largest number in an unordered list of n numbers. You'll notice below, as we move through the list there's only one element we need to keep track of. This element is the largest item we've seen up to that point. When we see a larger number we replace the tracked number with this new larger number.

No matter how many items we include in this list we would still only need to track a single number, so the space complexity of this algorithm is O(1). We might apply this algorithm to find the largest file on a computer.

In terms of time complexity if we were to add more files or more items to this list the amount of time it takes would increase proportionally to the number of items we add. We therefore say this algorithm has an O(n) time complexity.

If we wish to improve the time complexity of finding the largest file, we can do this by having something track the largest file in the systems and checks and updates this whenever a file is written. This would provide us with a constant time O(1) algorithm as we avoid having to check all the file sizes every time we request the largest file. The trade off here is added complexity when updating any file on our system. If we were to reduce the size of the largest file the second largest might now be the largest and we'd have to find which file that might be.

We don't often require knowing what the largest file on the system might be so this added complexity is probably a waste of resource, additionally the overhead of creating, updating and deleting files has now increased. An O(n) search is probably enough for most machines.

Sorting

Sorting is often used to explain time complexity as there are a number of ways to sort items each with their own complexity. It's also useful because we can visualise sorting. Below I have provided an example of bubble sort, this has a time complexity of O(n²).

This isn't the most efficient way to sort a list of items, but it's a good representation of an O(n²) algorithm.

Categorising complexity

So far we've been discussing polynomial time algorithms, there exist algorithms which take exponential time to produce a solution. As an example in the case we have 2 items this would take 4 operations, if we increase to 3 items it would take us 8 operations. Such an algorithm is said to have O(2ⁿ) time complexity.

An example of an exponential algorithmic problem is the N-Queens ii problem. The time complexity for an algorithm to solve this problem is O(n!). So 3 items is 6 operations, 4 items is 24 operations. These are algorithms which a computer would struggle to solve, in a sensible time, as n gets larger.

Within the realm of these exponential algorithms exist problems which we can solve in O(n!) time but we can validate the solution in polynomial time. So even if n is exceptionally large, given a solution, we are able to validate the correctness relatively quickly.

P vs NP

This class of algorithms forms the basis for one of the millennium problems, known as P vs NP. The problem asks if there's a relationship between the complexity of validating the solution and complexity in solving the problem. If P = NP then problems that can be verified in polynomial time can also be solvable in polynomial time. However P ≠ NP implies that some problems are inherently harder to solve than they are to verify.

There are a few problems which have no existing polynomial solution, which upon finding one will determine that P = NP. Problems such as the traveling salesman problem (TSP), The boolean satisfiability problem and the vertex cover problem Proving that there exists a polynomial solution to these problems will net you $1 million.

In Practice

Solving these problems have practical applications. Solving TSP would provide us optimal solutions for delivery routing and vertex cover has an application in DNA sequencing. So how do we produce solutions in these areas when attempting to find the best solution can take a computer as long as the lifetime of the universe.

We tend to rely on algorithms that are fast on average, these algorithms may involve backtracking with a large amount of pruning; this approach is used in chess. There are also approximation algorithms or heuristic based approaches such as simulated annealing.

Trade Offs

Understanding time and space allows us to make trade offs between strategies. Certain algorithms can provide us an efficient approach to solving technical problems. There is a limit to how much we can do with algorithms and sometimes even problems that sound simple on the surface could have a $1 million bounty standing for 25 years, without you realising it.