Binary search is quite a simple algorithm to explain and thus it is often one of the first algorithms computer scientists learn. It's also occasionally brought up in software engineering interviews as it can be applied when solving optimisation problems.

The traditional explanation of binary search is flawed and acts as a barrier to its application. Binary search is not an algorithm that believes a set can be divided into three groups, e.g. these numbers are too cold, these number are too hot and this number is just right.

This goldilocks framing of binary search forces us to look for situations where the problem contains an array of porridge ordered by temperature and we are in search of the one falls into our preferred consumption temperature.

Binary search is an algorithm that is optimal at finding state transitions and framing it as such opens up the application of binary search as we no longer approach problems like goldilocks and instead; finding the best porridge becomes finding the point at which the ordered bowls of porridge transition from being tepid to scolding.¹

The Basics

Commonly, binary search is introduced with the example of finding a word in a dictionary. As an example say we are tasked to find the word "Hippo":

The brute force approach is to start at A, and flick through the pages until you get to the page that contains "Hippo". This approach works, however the time complexity of this algorithm is O(n); where n is the number of pages in the dictionary. So in the worst case, "Zebra" or something, You're looking at all n pages.

Pretend H is Hippo:

n operations is not inherently bad. If you have a list of 10 words. n operations isn't going to harm you. It starts to get a bit much when you have a billion words and it's not practical when you have n words to find among a billion words.

Here's where we can apply binary search. If we want to find the word "Hippo". We start by jumping to a random page, or we open the book in the middle.² If the dictionary is 260 pages the middle will land us on 130 which will be M. We know that H is before M so we can throw away half the dictionary. M->Z, so from a single operation we've already chopped the worst case scenario to n/2. We don't stop here, now we go to page 65 (half of 130) which lands us somewhere between F and G we know H is after G so now we can pick something in between G -> M = J. We continue doing this, narrowing down the pages, until we land on the page that contains Hippo.

In the worst-case scenario, when we are looking in a dictionary of 260 pages, we do 9 operations. If we relied on the previous algorithm we would do 260 operations in the worst-case.

The Weaknesses

This explanation does a good job to help us understand the algorithm but it overcomplicates binary search as it breaks down the operations that binary search is doing into three parts.

1. Is the current word the word we are looking for?
2. Is the word we are looking for ahead of the current word?
3. Is the word we are looking for behind the current word?

These questions may help inform us as to how the algorithm behaves, but we can simplify it to the single binary question.

When does the word we are looking for no longer appear after our current word?

Instead of imaging the sequence as the words that might appear on each page, we can picture the sequence as the outcome of the statement: The word I'm looking for is after the current word.

As a result this frames binary search as a solution to finding a state transition. It is at the point when our word not longer appears after the current word that we find the word we are looking for.

Git Bisect

Binary search is used to find bugs. If you're familiar with git then you might have heard of git bisect. For those unfamiliar with git imagine a timeline with each point in that timeline being a change to a file. So every time the file is saved it adds a new node to the timeline.

Now instead of a single file, git works across a whole software project and each save is being noted down on the timeline. A change is what is being added and what is being removed, so the accumulated sum of all these changes is the current state of the project.

On large teams and complex projects bugs can occur after several changes have been made to the code. If we know that the code is broken in its current state but aren't sure what change caused the bug we can use git bisect to figure out which change is the culprit.

When we run git bisect we provide it with a point in time that we are certain no bug existed. git bisect will then present us a change between that time and now.

1. No bug
2. ?
3. ?
4. broken?
5. ?
6. ?
7. Bug

We then have to answer; is the software at point 4 broken? If yes, the bug was introduced between 1 and 4. This rules out all points after 4. Cutting the points we have to analyse down in half. git bisect continues, running a binary search over the changes in the project until we find the change on the timeline that introduced the bug.

Essentially we are using binary search to answer the statement: The bug exists, because we are interested when the state transitions from "The bug doesn't exist" to "The bug exists".

The Boolean Function

We can now separate binary search into two distinct parts. The algorithm part, which moves a pointer either up or down the timeline and the function that computes a boolean response. With this we can ask more interesting questions for which binary search provides an answer, as an example; "When did spend increase?" or "When did the user go into debt?".

We can even provide two arrays and find the answer for "When did trend A over take trend B", without computing the delta for all observations on the timeline.

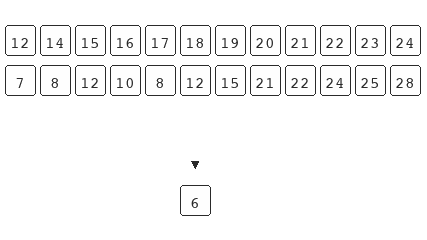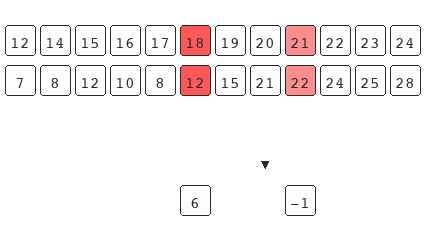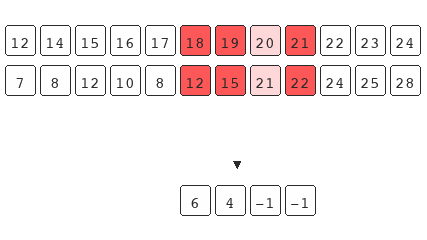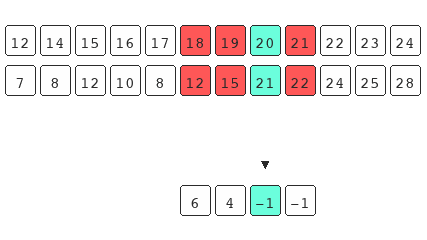
The main underlining assumption taught with the traditional explanation is that the set you're operating on should already be sorted for the search to work. The example above shows that this isn't true. Binary search only requires the underlying data to be bisect-able.

Binary search is an effective tool for these state transition problems. It is interesting that the algorithm on its own is easy to understand, the complexity and it's application seems to grow when you separate the algorithms iterator and the statement.

I'd be interested in finding out if the application of other algorithms grows when they're decomposed in a similar way.

Further reading

• Root Finding